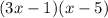Answer:
1.
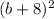
2.

3.
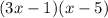
Explanation:
1. Both
 and 64 are perfect squares, meaning
and 64 are perfect squares, meaning
 is twice the product of x and 8. Since all signs are positive, the equation would be:
is twice the product of x and 8. Since all signs are positive, the equation would be:
 . Let
. Let
 and
and
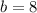 . Answer:
. Answer:
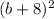 or
or
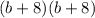 .
.
2. Since -3 is a factor of all 3 terms, factor out the -3 which makes,
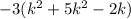 . K is also a common factor, so you would factor that out too,
. K is also a common factor, so you would factor that out too,
 . Then simply, find the two factors whose product is -2 and whose sum is -5. Answer:
. Then simply, find the two factors whose product is -2 and whose sum is -5. Answer:
 .
.
3. By factoring
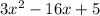 , you would break the expressions in the group=
, you would break the expressions in the group=
 . Then, factor out "x" from
. Then, factor out "x" from
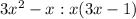 . Factor out "5" from
. Factor out "5" from
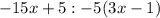 =
=
 . Finally, factor out the common term "3x-1" =
. Finally, factor out the common term "3x-1" =