Question

Suppose a researcher is trying to understand whether people who purchase fast-food hamburgers would be willing to pay more if the hamburger comes with a free whistle. Prior research suggests the mean amount customers say they are willing to pay for a hamburger is μ = 3.68 and σ = 0.70. The researcher plans to conduct a study very similar to the prior research by selecting a sample of customers and asking them how much they are willing to pay for the hamburger. Before asking, however, she will tell the customer about the free whistle that will come with the hamburger. The researcher’s null hypothesis is that the mean amount the customers are willing to pay when they are told about the free whistle is no different than the amount customers are willing to pay when they are not told they will receive a free whistle. The researcher’s sample of 49 customers has a sample mean of M = 4.04. The test statistic for this sample mean is 3.60. Using a significance level of α = .05, which of the following is the most appropriate statement of the result?

a. Telling customers they will receive a free cookie with their hamburger had a significant effect on the amount they say they are willing to pay for a hamburger, z = 3.68, p < .05.
b. Telling customers they will receive a free cookie with their hamburger did not have a significant effect on the amount they say they are willing to pay for a hamburger, z = 4.04, p > .05.
c. Telling customers they will receive a free cookie with their hamburger had a significant effect on the amount they say they are willing to pay for a hamburger, z = 3.60, p < .05.
d. Telling customers they will receive a free cookie with their hamburger did not have a significant effect on the amount they say they are willing to pay for a hamburger, z = 3.60, p < .05

Answer 1

Option c. Telling customers they will receive a free cookie with their hamburger had a significant effect on the amount they say they are willing to pay for a hamburger, z = 3.60, p < .05 .

Explanation:

We are given that Prior research suggests the mean amount customers say they are willing to pay for a hamburger is μ = 3.68 and σ = 0.70.

Here, Null Hypothesis,
`H_0` :
`\mu` = 3.68 {means that the mean amount the customers are willing to pay when they are told about the free whistle is no different than the amount customers are willing to pay when they are not told they will receive a free whistle}

Alternate Hypothesis,
`H_1` :
`\mu \\eq` 3.68 {means that the mean amount the customers are willing to pay when they are told about the free whistle is different than the amount customers are willing to pay when they are not told they will receive a free whistle}

The test statistics that will be used here is;

T.S. =
`(Xbar-\mu)/((\sigma)/(√(n) ) )` ~ N(0,1)

where, Xbar = sample mean = 4.04

`\sigma` = population standard deviation = 0.70

`\mu` = population mean = 3.68

n = sample customers = 49

So, test statistics =
`(4.04-3.68)/((0.70)/(√(49) ) )`

= 3.60

P-value is given by = P(Z > 3.60) = 1 - P(Z <= 3.60)

= 1 - 0.99984 = 0.00016

Since our p-value is less than the significance level of 0.05, so we have sufficient evidence to reject null hypothesis.

Therefore, we conclude that the mean amount the customers are willing to pay when they are told about the free whistle is different than the amount customers are willing to pay when they are not told they will receive a free whistle.

Answer 2

Correct option (c).

Explanation:

The experiment consists of determining whether the people who purchase fast-food hamburgers would be willing to pay more if the hamburger comes with a free whistle.

The hypothesis for this test is defined as:

H₀: The mean amount the customers are willing to pay when they are told about the free whistle is no different than the amount customers are willing to pay when they are not told they will receive a free whistle, i,e. μ = 0.

Hₐ: The mean amount the customers are willing to pay when they are told about the free whistle is different than the amount customers are willing to pay when they are not told they will receive a free whistle, i,e. μ ≠ 0.

The significance level of the test is, α = 0.05.

The test statistic is defined as:

`z=(\bar x-\mu)/(\sigma/√(n))`

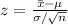
The value of test statistic is, z = 3.60.

Decision rule:

If the p-value of the test statistic is less than the significance level then the null hypothesis will be rejected and vice versa.

The p-value of the test is,

`p-value=2P(Z>3.60)\\=2[1-P(Z<3.60)]\\=2[1-0.9998]\\=0.0004`

*Use a z-table for the probability.

The p-value = 0.0004 < α = 0.05.

The null hypothesis will be rejected since the p-value is less than the significance level.

Conclusion:

Telling customers they will receive a free whistle with their hamburger had a significant effect on the amount they say they are willing to pay for a hamburger, z = 3.60, p < .05.