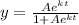Answer:
Therefore ,
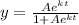
Explanation:
The fraction of population who have heard rumor = y
The fraction of population who haven't heard rumor = 1-y
The rate of of spread (y'(t)) is proportional to the product of the fraction of population who have heard rumor the fraction of population who have heard rumor.
Therefore
y'(t) ∝ y (1-y)
⇒ y'(t) =k y (1-y) [ k = constant of proportional]


Integrating both sides
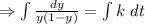
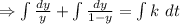
![[\because (1)/(y(1-y)=(1)/(y)+(1)/(1-y) ]](https://img.qammunity.org/2021/formulas/mathematics/college/5yo9rd8iw0t4gnlnhsu24dd2y10m695zs5.png)
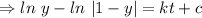 [ c = arbitrary constant]
[ c = arbitrary constant]

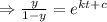
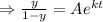 [ Here
[ Here
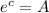 ]
]
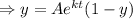

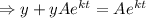
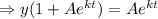
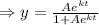
Therefore ,