Question

Assume that the pre-worker production function is yt = 2kt^0.5. The saving and depreciation rete retes are estimated at 0.2 and 0.04, respectively.

a. Calculate the capital-labor ratio steady state for this economy.

b. Calculate consumption per worker at the steady state.

Answer 1

a) K_t 100

b) Y_t = 200

Step-by-step explanation:

When the economy is at steady state then, it will grow at zero it is only replacing for the depreciate capital.

So, savings times income (investment) matches Capital times depreciation rate

`S * Y_t = d * K`

`0.2(2K_t^(0.5))= 0.04K_t\\0.4K_t^(0.5) = 0.04K_t\\K_t = ((0.04K_t)/(0.4))^2 \\K_t = 0.01K_t^2\\\\0 = 0.01K_t^2 - K_t\\$We solve the root: K_t = 100`

(The previous istep is made with the quadratic formula)

second question:

Now, we solve for C per worker at this rate

`Y_t= 2K_t^(0.5)\\Y_t = 2(100)^(0.5)\\\\Y_t = 20`

Answer 2

(A). It is given that the production function is
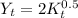`Y_(t) = 2K_(t)^(0.5)`. All the variables are in per workers terms. Like y) is output per worker and lu is the capital-labor ratio.

The Depreciation rate is
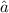`∞` = 0.04 and the Savings rate is
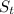`S_(t)` = 0.2

a) At steady-state the change in capital is zero. The calculation of capital-labor ratio given steady state is as follows:

Δk = 0

`SY_(t) - ∞K_(t) = 0`

`0.2(2K_(t)^(0.5) ) = 0.04K_(t)`

`0.4K_(t)^(0.5) = 0.04K_(t)`

`K_(t) = 100`

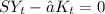
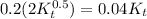
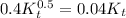
Thus, the steady-state value of the capital-labor ratio is
`K_(t) = 100`

(b) to calculate consumption per worker, first calculate the output per worker and then calculate the consumption per worker. The calculations are as follows:

`Y_(t) = 2K_(t)^(0.5)`

`Y_(t) = 2(100)^(0.5)`

`Y_(t) = 2(10)`

`Y_(t) = 20`

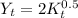
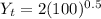
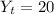
The output per worker is 20

The calculation of steady-state value of the consumption per worker is as follows

C= (1—s) y

C = (1— 0.2)20

C= 0.8 x 20

C = 16

Thus, the consumption per worker at the steady state is 16