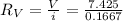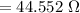Answer:
The minimum value is
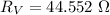
Step-by-step explanation:
From the question we are given that
The voltage is
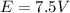
The internal resistance is
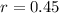
The objective of this solution is to obtain the minimum value of the voltmeter resistance for which the voltmeter reading is within 1.0% of the emf of the battery
What is means is that we need to obtain voltmeter resistance such that
V = (100% -1%) of E
Where E is the e.m.f of the battery and V is the voltmeter reading
i.e V = 99% of E = 0.99 E = 7.425
Generally
E = V + ir
where ir is the internal potential difference of the voltmeter and
V is the voltmeter reading
Making i the subject of the formula above
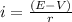
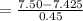
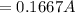
Now the current is constant through out the circuit so,
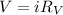
Where
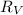 is the value of voltmeter resistance
is the value of voltmeter resistance
Hence