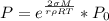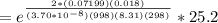Question

Calculate the vapor pressure for a mist of spherical water droplets of radius 3.70×10−8m surrounded by water vapor at 298 K. The vapor pressure of water at this temperature is 25.2 Torr, the density of water is 998 kg⋅m−3, and the surface tension of water is 71.99 mN⋅m−1.

Answer 1

The vapor pressure for a mist is
`P= 25.92\ Torr`

Step-by-step explanation:

From the question we are given that

The radius is
`r = 3.70 *10^(-8) m`

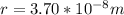
The temperature is
`T = 298K`

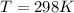
The vapor pressure of water
`P_o = 25.2\ Torr`

The density of water is
`\rho = 998 kg.m^(-3)`

The surface tension of water is
`\sigma = 71.99 m N \cdot m^(-1)`

Generally the equation of that is mathematically represented as

`ln ((P)/(P_0) ) = (2 \sigma M)/(r \rho RT)`

Where P is the vapor pressure for mist

R is the ideal gas constant = 8.31

making P the subject in the formula

`P = e^ {(2 \sigma M)/(r \rho RT)} * P_0`

`= e^{(2 *(0.07199)(0.018))/((3.70*10^(-8))(998)(8.31)(298)) } * 25.2`

`P= 25.92Torr`