Answer:
210,600πft-lb
Step-by-step explanation:
Force is a function F(x) of position x then in moving from
x = a to x= b
Work done =
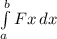
Consider a water tank conical in shape
we will make small horizontal section of the water at depth h and thickness dh and also assume radius at depth h is w
we will have ,
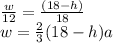
weight of slice under construction
weight = volume × density × gravitational constant
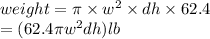
Now we can find work done

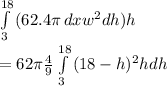
=
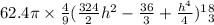
= 210,600πft-lb