Question

A consumer organization collected data on two types of automobile batteries, A and B. The summary statistics for 12 observations of each type are . X(bar)A=36.51, X(bar)B=34.21, SA=1.43, SB=.93. Assume that the data are normally distributed with OA=OB.

Is there evidence to support the claim that type A battery mean life exceeds that of type B? Test the hypothesis at alpha = 0.05

Construct a 99% Confidence interval (CI) for the difference in the mean battery life.

Answer 1

There evidence to support the claim that type A battery mean life exceeds that of type B.

The 99% Confidence interval (CI) for the difference in the mean battery life is (0.91, 3.69).

Explanation:

The hypothesis can be defined as follows:

H₀:The mean life of battery A is not more than that of battery B, i.e.
`\mu_(A)-\mu_(B)\leq 0`.

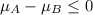Hₐ:The mean life of battery A is more than that of battery B, i.e.
`\mu_(A)-\mu_(B)>0`.

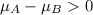The significance level of the test is, α = 0.05.

The test statistic is:

`t=(\bar x_(A)-\bar x_(B))/(SE)`

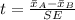
Compute the value of standard error as follows:

`SE=\sqrt{(s_(A)^(2))/(n_(A))+(s_(B)^(2))/(n_(B))}=\sqrt{(1.43^(2))/(12)+(0.93^(2))/(12)}=√(0.242483)=0.4924`

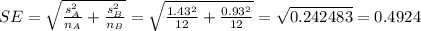
Compute the test statistic as follows:

`t=(\bar x_(A)-\bar x_(B))/(SE)=(36.51-34.21)/(0.4924)=4.67`

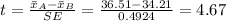
Decision rule:

If the test statistic value is more than the critical value,
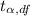`t_(\alpha, df)`, then the null hypothesis will be rejected. And vice-versa.

Compute the degrees of freedom (df) as follows:

`df=(SE^(4))/(((s_(A)^(2)/n_(A))^(2))/(n_(A)-1)+((s_(B)^(2)/n_(B))^(2))/(n_(B)-1))=(0.4924^(4))/(0.022)=18.88\approx19`

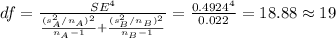
The critical value is,
`t_(\alpha, df)=t_(0.05, 19)=1.729`

The test statistic, t = 4.67 >
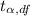`t_(\alpha, df)` = 1.729.

Thus, the null hypothesis is rejected at 5% level of significance.

Conclusion:

Thus, there evidence to support the claim that type A battery mean life exceeds that of type B.

The critical value of t for a 99% confidence level and degrees of freedom 19 is:

`t_(0.01/2, 22)=2.819`

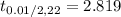
The pooled standard deviation is:

`S_(p)^(2)=((n_(A)-1)s_(A)^(2)+(n_(B)-1)s_(B)^(2))/(n_(A)+n_(B)-2)=((11*1.43^(2))+(11*0.93^(2)))/(22)=1.455`

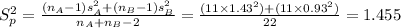
Compute the 99% confidence interval for the difference in the mean battery life as follows:

`CI=\bar x_(A)-\bar x_(B)\pm t_(00.01/2, 22)* \sqrt{S_(p)^(2)[(1)/(n_(A))+(1)/(n_(B))]}\\=(36.51-34.21)\pm 2.819*\sqrt{1.455[(1)/(12)+(1)/(12)]}\\=2.3\pm1.39\\=(0.91, 3.69)`

Thus, the 99% Confidence interval (CI) for the difference in the mean battery life is (0.91, 3.69).