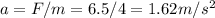Question

A 4.0 kg block is pushed along a horizontal floor by a force F→ of magnitude 26 N at a downward angle θ = 40°. The coefficient of kinetic friction between the block and the floor is 0.24. Calculate the magnitudes of (a) the frictional force on the block from the floor and (b) the block’s acceleration.

Answer 1

(a) 13.43 N

(b) 1.62 m/s2

Step-by-step explanation:

(a)Let g = 9.81 m/s2

The pushing force can be split into 2 components: 1 parallel and the other perpendicular to the floor:

- The parallel component:
`F_a = Fcos\theta = 26*cos40^o = 19.92 N`

- The perpendicular component:
`F_e = Fsin\theta = 26sin40^o = 16.7 N`

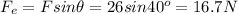
Friction force is the product of coefficient and normal force, which consists of gravity and the perpendicular pushing force

`F_f = \mu N = \mu (F_g + F_e) =\mu (mg + F_e)`

`F_f = 0.24(4*9.81 + 16.7) = 13.43 N`

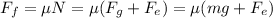
(b) Horizontally speaking, the net force acting on the block is the parallel force subtracted by friction

`F = F_e - F_f = 19.92 - 13.43 = 6.5 N`

The block acceleration according to Newton's 2nd law is

`a = F/m = 6.5 / 4 = 1.62 m/s^2`