Question

A survey asks a random sample of 1500 adults in Ohio if they support an increase in the state sales tax from 5% to 6%, with the additional revenue going to education. Let ^ p denote the proportion in the sample who say they support the increase. Suppose that 24% of all adults in Ohio support the increase. The standard deviation of the sampling distribution is . Round your answer to four decimal places.

Answer 1

Answer: The standard deviation of the sampling distribution is 0.0110

Explanation:

The standard deviation of the sampling distribution is given by :-

`s=\sqrt{(p(1-p))/(n)}`

, where p = population proportion and n = sample size.

Let
`\hat{p}` denote the proportion in the sample who say they support the increase.

As per given :

`\hat{p}=24\%=0.24`

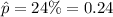
Then , the standard deviation of the sampling distribution is

`s=\sqrt{(0.24(1-0.24))/(1500)}=√(0.0001216)\approx0.0110`

Hence, the standard deviation of the sampling distribution is 0.0110.