Answer:
(a) Probability that a visually impaired student gets less than 6.2 hours of sleep is 0.10204 .
Explanation:
We are given that Researchers found that visually impaired students averaged 9.54 hours of sleep, with a standard deviation of 2.62 hours. Assume that the number of hours of sleep for these visually impaired students is normally distributed.
Let X = number of hours of sleep
So, X ~ N(
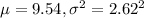 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean = 9.54 hours
= population mean = 9.54 hours
 = standard deviation = 2.62 hours
= standard deviation = 2.62 hours
So, the probability that a visually impaired student gets less than 6.2 hours of sleep is given by = P(X < 6.2)
P(X < 6.2) = P(
 <
<
 ) = P(Z < -1.27) = 1 - P(Z
) = P(Z < -1.27) = 1 - P(Z
 1.27)
1.27)
= 1 - 0.89796 = 0.10204
Therefore, the probability that a visually impaired student gets less than 6.2 hours of sleep is 0.10204.