Answer:
z test statistic is -1.042 .
Explanation:
We are given that based on the Nielsen ratings, the local CBS affiliate claims its 11 p.m. newscast reaches 41% of the viewing audience in the area. In a survey of 100 viewers, 36% indicated that they watch the late evening news on this local CBS station.
Let Null Hypothesis,
 : p = 0.41 {means that % of the viewing audience in the area is 41%}
: p = 0.41 {means that % of the viewing audience in the area is 41%}
Alternate Hypothesis,
 : p
: p
 0.41 {means that % of the viewing audience in the area is different from 41%}
0.41 {means that % of the viewing audience in the area is different from 41%}
The z-test statistics we will use here is One sample proportion test ;
T.S. =
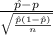 ~ N(0,1)
~ N(0,1)
where, p = % of the viewing audience based on the Nielsen ratings = 41%
 = % of the viewing audience based on a survey of 100 viewers = 36%
= % of the viewing audience based on a survey of 100 viewers = 36%
n = sample of viewers = 100
So, test statistics =
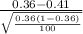
= -1.042
Therefore, the z test statistic is -1.042 .