Question

The life in hours of a biomedical device under development in the laboratory is known to be approximately normally distributed. A random sample of 15 devices is selected and found to have an average life of 5323.8 hours and a sample standard deviation of 220.9 hours.

Test the hypothesis that the true mean life of a biomedical device is greater than 5200.

Answer 1

We conclude that the true mean life of a biomedical device is greater than 5200 hours.

Explanation:

We are given that the life in hours of a biomedical device under development in the laboratory is known to be approximately normally distributed. For this a random sample of 15 devices is selected and found to have an average life of 5323.8 hours and a sample standard deviation of 220.9 hours.

We have to test that the true mean life of a biomedical device is greater than 5200 or not.

Let, Null Hypothesis,
`H_0` :
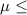`\mu \leq` 5200 {means that the true mean life of a biomedical device is less than or equal to 5200 hours}

Alternate Hypothesis,
`H_1` :
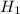`\mu` > 5200 {means that the true mean life of a biomedical device is greater than 5200 hours}

The test statistics that will be used here is;

T.S. =
`(Xbar-\mu)/((s)/(√(n) ) )` ~
`t_n_-_1`

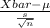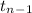
where, Xbar = sample average life = 5323.8 hours

s = sample standard deviation = 220.9 hours

n = sample devices = 15

So, test statistics =
`(5323.8-5200)/((220.9)/(√(15) ) )` ~
`t_1_4`

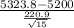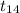
= 2.171

Since, we are not given with the significance level, so we assume it to be 5%, now the critical value of t at 14 degree of freedom in t table is given as 1.761. Since our test statistics is more than the critical value of t which means our test statistics will lie in the rejection region. So, we have sufficient evidence to reject our null hypothesis.

Therefore, we conclude that the true mean life of a biomedical device is greater than 5200 hours.