The car is about 6.6 years old.
Explanation:
Given : An equation for the depreciation of a car is given by
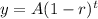 , where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years. The value of a car is half what it originally cost. The rate of depreciation is 10%.
, where y = current value of the car, A = original cost, r = rate of depreciation, and t = time, in years. The value of a car is half what it originally cost. The rate of depreciation is 10%.
To find : Approximately how old is the car?
Solution :
The value of a car is half what it originally cost i.e.
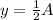
The rate of depreciation is 10% i.e. r=10%=0.1
Substitute in the equation,
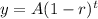
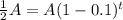
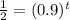
Taking log both side,
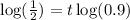
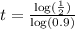
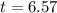
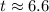
Therefore, the car is about 6.6 years old.