Question

A vertical scale on a spring balance reads from 0 to 200 N . The scale has a length of 11.0 cm from the 0 to 200 N reading. A fish hanging from the bottom of the spring oscillates vertically at a frequency of 2.55 Hz .Ignoring the mass of the spring, what is the mass m of the fish?

Answer 1

7.08 kg

Step-by-step explanation:

Given:

Length of scale (x) = 11.0 cm = 0.110 m [1 cm = 0.01 m]

Range of scale is from 0 to 200 N.

Frequency of oscillation of fish (f) = 2.55 Hz

Mass of the fish (m) = ?

Now, range of scale is from 0 to 200 N. So, maximum force, the spring can hold is 200 N. For this maximum force, the extension in the spring is equal to the length of the scale. So,
`x = 0.11\ m`

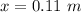
Now, we know that, spring force is given as:

`F=kx\\\\k=(F)/(x)`

Where, 'k' is spring constant.

Now, plug in the given values and solve for 'k'. This gives,

`k=(200\ N)/(0.11\ m)=1818.18\ N/m`

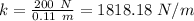
Now, the oscillation of the fish represents simple harmonic motion as it is attached to the spring.

So, the frequency of oscillation is given as:

`f=(1)/(2\pi)\sqrt{(k)/(m)}`

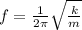
Squaring both sides and expressing it in terms of 'm', we get:

`(k)/(m)=4\pi^2f^2\\\\m=(k)/(4\pi^2f^2)`

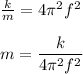
Now, plug in the given values and solve for 'm'. This gives,

`m=(1818.18\ N/m)/(4\pi^2* (2.55\ Hz)^2)\\\\m=(1818.18\ N/m)/(256.708\ Hz^2)\\\\m=7.08\ kg`

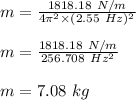
Therefore, the mass of the fish is 7.08 kg.