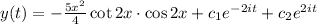Question

Set up but do not solve for the appropriate particular solution yp for the differential equation y′′+4y=5xcos(2x) using the Method of Undetermined Coefficients (primes indicate derivatives with respect to x). In your answer, give undetermined coefficients as A, B, etc.

Answer 1

So, solution of the differential equation is

`y(t)=-(5x^2)/(4)\cot 2x\cdot \cos 2x+c_1e^(-2it)+c_2e^(2it)\\`

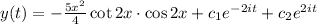
Explanation:

We have the given differential equation: y′′+4y=5xcos(2x)

We use the Method of Undetermined Coefficients.

We first solve the homogeneous differential equation y′′+4y=0.

`y''+4y=0\\\\r^2+4=0\\\\r=\pm2i\\\\`

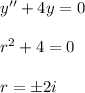
It is a homogeneous solution:

`y_h(t)=c_1e^(-2i t)+c_2e^(2i t)`

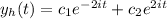
Now, we finding a particular solution.

`y_p(t)=A5x\cos 2x\\\\y'_p(t)=A5\cos 2x-A10x\sin 2x\\\\y''_p(t)=-A20\sin 2x-A20x\cos 2x\\\\\\\implies y''+4y=5x\cos 2x\\\\-A20\sin 2x-A20x\cos 2x+4\cdot A5x\cos 2x=5x\cos 2x\\\\-A20\sin 2x=5x\cos 2x\\\\A=-(x)/(4) \cot 2x\\`

we get

`y_p(t)=A5\cos 2x\\\\y_p(t)=-(5x^2)/(4)\cot 2x\cdot \cos 2x\\\\\\y(t)=y_p(t)+y_h(t)\\\\y(t)=-(5x^2)/(4)\cot 2x\cdot \cos 2x+c_1e^(-2it)+c_2e^(2it)\\`

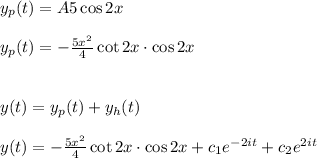
So, solution of the differential equation is

`y(t)=-(5x^2)/(4)\cot 2x\cdot \cos 2x+c_1e^(-2it)+c_2e^(2it)\\`