Question

A circle has a circumference of 6. It has an arc of length 17/3. What is the central angle of the arc, in degrees?

Answer 1

340 degrees

Explanation:

So the key thing here is to notice that we are given the circumference which will allow us to find a value for the radius of the circle and hence the angle subtended by the arc (the central angle).

So the circumference of a circle = 2pi(r)

This means:

6 = 2pi(r)

Which means that

r = 6/2pi or r = 3/pi

Now we can use this value of r to find our angle in conjunction with the value of the arc length. So:

Arc length is defined by: length = θr

Where θ is our angle value.

So lets plug in:

`(17)/(3) = (angle)(3)/(\pi )`

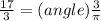
Multiply by pi to get:

`(17\pi )/(3) = 3(angle)`

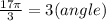
Divide by 3 to get that:

θ = 17pi/9

So if we convert that from radians to degrees we get 340 degrees.