Hi there!
We can use Ampère's Law:
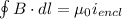
B = Magnetic field strength (B)
dl = differential length element (m)
μ₀ = Permeability of free space (T/Am)
Since this is a closed-loop integral, we must integrate over a closed loop. We can integrate over a rectangular-enclosed area of the rim of the solenoid - ABCD - where AD and BC are perpendicular to the solenoid.
Thus, the magnetic field is equivalent to:
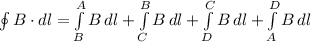
Since AD and BC are perpendicular, and since:
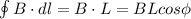
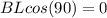
If perpendicular to the field, the equation equals 0.
Additionally, since AB is outside of the solenoid, there is no magnetic field present, so B = 0. The only integral we integrate now is:
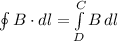
Which is horizontal and inside the solenoid. Let the distance between C and D be 'L', and the enclosed current is equivalent to the number of loops multiplied by the current:
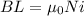
N = # of loops per length multiplied by the length, so:
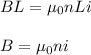
Plug in the given values and solve. Remember to convert # of loops to # of loops per unit length.
