Question

In a recent year, potentially dangerous commercial aircraft incidents (e.g., near collisions) averaged 1.2 per 100,000 flying hours. Let X be the number of incidents in a 100,000-hour period. (a) Justify the use of the Poisson model. Near collisions are random and independent events. Each collision is dependent on the occurrence of another. Collisions are routine systematic occurrences. (b) What is the probability of at least one incident? (Round your answer to 4 decimal places.) Probability (c) More than three incidents? (Round your answer to 4 decimal places.) Probability

Answer 1

a) Near collisions are random and independent events.

b) P=0.6988

c) P=0.1205

Explanation:

a) The use of a Poisson model is appropiate because it can represent independent events subject to a usually low occurrence rate and high exposure (in number of hours, in this example). Near collisions are random and independent events.

b) The rate of occurrence is 1.2 near collisions per 100,000 flying hours.

`\lambda=1.2`

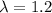
The probability of at least one incident is:

`P(X\geq 1)=1-P(0)=1-(\lambda^0e^(-\lambda))/(0!) \\\\P(X\geq 1)=1-e^(-1.2)=1-0.3012=0.6988`

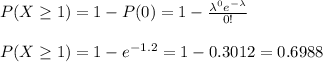
c) The probability of more than 3 incidents is:

`P(X>3)=1-(P(0)+P(1)+P(2))\\\\P(X>3)=1-(0.3012+0.3614+0.2169)=1-0.8795=0.1205\\\\\\P(0)=0.3012\\\\P(1)=(1.2^1e^(-1.2))/(1!)=1.2*0.3012=0.3614\\\\P(2)=(1.2^2e^(-1.2))/(2!)= 1.44*0.3012/2=0.2169`