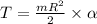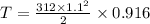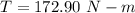Answer:172.90 N-m
Step-by-step explanation:
Given
mass of merry-go-round

radius of disk
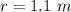
Final angular speed
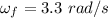
time
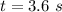
initial angular speed
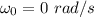
using
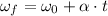
where
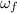 =final angular speed
=final angular speed
 =Initial angular speed
=Initial angular speed
 =angular speed
=angular speed
 =time
=time
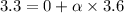
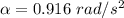
Torque can be written by

where I=moment of Inertia