Answer:
P-value = 0.999 ; Conclusion = Do not reject

Explanation:
We are given that a student believes that less than 50% of students at his college receive financial aid. A random sample of 120 students was taken. Sixty-five percent of the students in the sample receive financial aid.
Let Null Hypothesis,
 : p
: p
 0.50 {means that more than or equal to 50% of students at his college receive financial aid}
0.50 {means that more than or equal to 50% of students at his college receive financial aid}
Alternate Hypothesis,
 : p < 0.50 {means that less than 50% of students at his college receive financial aid}
: p < 0.50 {means that less than 50% of students at his college receive financial aid}
The test statics that will be used here is One-sample proportions test;
T.S. =
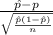 ~ N(0,1)
~ N(0,1)
where,
 = % of the students in the sample that receive financial aid = 65%
= % of the students in the sample that receive financial aid = 65%
n = sample of students = 120
So, test statistics =
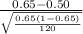
= 3.45
Now, at 0.02 level of significance the z table gives critical value of -2.054. Since our test statistics is more than the critical value of z so we have insufficient evidence to reject null hypothesis as it will not fall in the rejection region.
P-value is given by = P(Z < 3.45) = 0.99972 or 0.999 {using z table}
So, we conclude that null hypothesis is not rejected and p-value is 0.999.