Answer:
The probability that a radio selected at random will last from 600 to 700 hours is 0.3413
Explanation:
The playing life of a Sunshine radio is normally distributed
Mean =
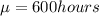
Standard deviation =
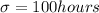
We are supposed to find the probability that a radio selected at random will last from 600 to 700 hours i.e.P(600<x<700)
Formula:
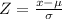
At x = 600
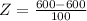
Z=0
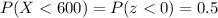
At x = 700
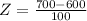
Z=1

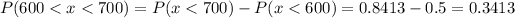
Hence the probability that a radio selected at random will last from 600 to 700 hours is 0.3413