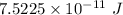Answer:
(a). The charge is

(b). The initial stored energy is
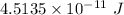
(c). The final stored energy is

(d). The work required to separate the plates is
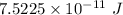
Step-by-step explanation:
Given that,
Area = 8.50 cm²
Distance = 3.00 mm
Potential = 6.00 V
Distance without discharge = 8.00 mm
(a). We need to calculate the capacitance
Using formula of capacitance
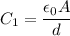
Put the value into the formula
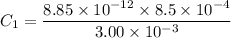

We need to calculate the charge
Using formula of charge
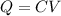
Put the value into the formula
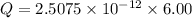

(b). We need to calculate the initial stored energy
Using formula of initial energy
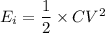
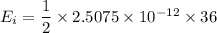

(c). We need to calculate the capacitance
Using formula of capacitance
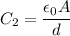
Put the value into the formula
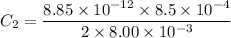
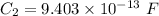
We need to calculate the final stored energy
Using formula of initial energy
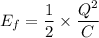
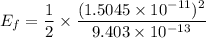
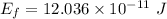
(d). We need to calculate the work done
Using formula of work done
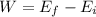
Put the value in the formula
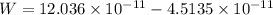

Hence, (a). The charge is

(b). The initial stored energy is
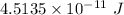
(c). The final stored energy is

(d). The work required to separate the plates is