Question

An English teacher needs to pick 10 books to put on her reading list for the next school year, and she needs to plan the order in which they should be read. She has narrowed down her choices to 4 novels, 6 plays, 8 poetry books, and 4 nonfiction books. Step 1 of 2: If she wants to include no more than 3 poetry books, how many different reading schedules are possible? Express your answer in scientific notation rounding to the hundredths place. Answer Tables II Keypa a x10

Answer 1

The number of possible different reading schedules is
`2.93*10^5`.

Explanation:

She can pick 10 books from 8 poetry books and (4 + 6 + 4 =) 14 others.

She has to pick no more than 3 poetry books.

She could pick

1. 0 poetry books and 10 of the others
2. 1 poetry book and 9 others
3. 2 poetry books and 8 others
4. 3 poetry books and 7 others

The number of ways =
`[\binom{8}{0} * \binom{14}{10}]+[\binom{8}{1} * \binom{14}{9}]+[\binom{8}{2} * \binom{14}{8}]+[\binom{8}{3} * \binom{14}{7}]`

=
`(1*1001) + (8*2002)+(28*3003)+(56*3432) = 293293`

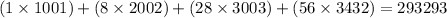
In scientific notation, this is
`2.93*10^5`.