Question

Each side of a square is increasing at a rate of 8 cm/s. At what rate is the area of the square increasing when the area of the square is 25 cm2?

Answer 1

80cm^2/s

Explanation:

This is a related rates problem where we are considering the rate at which the area of a square changes with respect to time.

So lets consider the area of a square:

A = s^2 (where s represents the length of one side of the square)

Related rates problem deal with functions of time so if we take the area and side length as a function of time and then differentiate implicitly we get:

`(dA)/(dt) = 2s((ds)/(dt))`

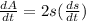
The problem states that the side of a square is increasing at a rate off 8cm/s so we can conclude that ds/dt = 8cm/s leaving us with:

`(dA)/(dt) = 16s`

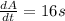
Now, to solve for s we have to consider the other value given. If the area of the square is initially 25cm^2 we can plug this into our formula for area to solve for the side length.

25 = s^2

s = +/- 5 (since side lengths are only positive we only consider +5)

s = 5

Now we can plug this back in for s:

`(dA)/(dt) = 80`

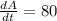
Therefore, the rate at which the area of the square is increasing is 80cm^2 per second.