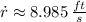Question

man starts walking north at 2 ft/s from a point P. Five minutes later a woman starts walking south at 7 ft/s from a point 500 ft due east of P. At what rate are the people moving apart 15 min after the woman starts walking? (Round your answer to two decimal places.)

Answer 1

`\dot r \approx 8.985\,(ft)/(s)`

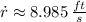
Explanation:

Let consider that vertical axis has its positive side oriented to the north and positive side of the horizontal axis has its orientation to the east. Besides, both persons walk at constant rate. Then, displacement formulas are:

Man

`y_(1) = (2\,(ft)/(s))\cdot t`

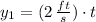
Woman

`y_(2) = - (7\,(ft)/(s) )\cdot (t-300\,s)`

The minimum distance between the man and the woman can be calculated by means of the Pythagorean Theorem:

`r=\sqrt{(500\,ft)^(2)+(y_(1)-y_(2))^(2)}`

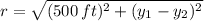
The rate of change of such distance is:

`\dot r = \frac{(y_(1)-y_(2))\cdot (\dot y_(1)-\dot y_(2))}{\sqrt{(500\,ft)^(2)+(y_(1)-y_(2))^(2)}}`

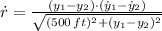
The positions and velocities at
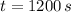`t = 1200\,s` are:

`y_(1) = 2400\,ft`

`\dot y_(1) = 2\,(ft)/(s)`

`y_(2) =-6300\,ft`

`\dot y_(2) = -7\,(ft)/(s)`

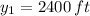
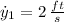
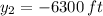
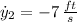
The rate of change is:

`\dot r \approx 8.985\,(ft)/(s)`