Answer:
The proportion of young adults (18-25 years of age) in a certain city in the U.S. are not different from the proportion of the general population of young adults in the U.S.
Explanation:
The hypothesis for the test can be defined as:
H₀: The proportion of young adults (18-25 years of age) in a certain city in the U.S. are not different from the actual proportion, i.e. P = p.
Hₐ: The proportion of young adults (18-25 years of age) in a certain city in the U.S. are different from the actual proportion, i.e. P ≠ p.
The test statistic is defined as:
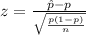
Assume that the significance level of the test is, α = 0.05.
The decision rule is:
If the p-value of the test is less than the significance level then the null hypothesis will be rejected. And vice-versa.
It is provided that the p-value of the test is, p-value = 0.076.
The p-value = 0.076 > α = 0.05.
Thus, the null hypothesis will not be rejected at 5% level of significance.
Conclusion:
The proportion of young adults (18-25 years of age) in a certain city in the U.S. are not different from the proportion of the general population of young adults in the U.S.