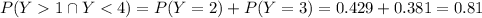Question

Four diners have ordered a platter of desserts. The platter holds 8 chocolate chip cookies and 4 slices of chocolate cheesecake. The waiter gives each diner a randomly selected dessert. Let Y = the number of slices of cheesecake left on the platter after the first serving. The distribution of Y is Y 0 1 2 3 4 P(Y) 0.005 0.114 0.429 0.381 0.071 Find the probability that there's more than one slice left, but not all of them are left, i.e.,

Answer 1

`P(Y>1 \cap Y<4)`

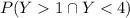
And we can find this probability like this:

`P(Y>1 \cap Y<4)= P(Y=2) +P(Y=3)`

And we can replace the values and we got:

`P(Y>1 \cap Y<4)= P(Y=2) +P(Y=3)=0.429 +0.381 = 0.81`

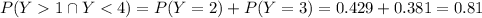
Explanation:

For this case we define the random variable Y as: the number of slices of cheesecake left on the platter after the first serving. And we have the following distribution for Y:

Y | 0 1 2 3 4

P(Y) | 0.005 0.114 0.429 0.381 0.071

And we want to find the following probability:

`P(Y>1 \cap Y<4)`

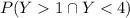
And we can find this probability like this:

`P(Y>1 \cap Y<4)= P(Y=2) +P(Y=3)`

And we can replace the values and we got:

`P(Y>1 \cap Y<4)= P(Y=2) +P(Y=3)=0.429 +0.381 = 0.81`