Answer:
0.1308
Step-by-step explanation:
To keep the rider from sliding down, then the friction force
 must at least be equal to gravity force
must at least be equal to gravity force

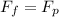
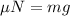
where μ is the coefficient, N is the normal force acted by the rotating cylinder, m is the mass of a person and g = 9.81 m/s2 is the gravitational acceleration.
According to Newton's 3rd and 2nd laws, the normal force would be equal to the centripetal force
 , which is the product of centripetal acceleration
, which is the product of centripetal acceleration
 and object mass m
and object mass m
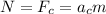
Therefore
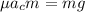
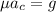
The centripetal acceleration is the ratio of velocity squared and the radius of rotation
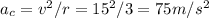
Therefore
