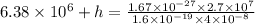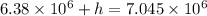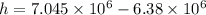Question

A proton is circling the Earth above the magnetic equator, where Earth’s magnetic field is directed horizontally north and has a magnitude of 4.00 × 10–8 T. If the proton is moving at a speed of 2.7 × 107 m/s, how far above the surface of the Earth is the proton

Answer 1

`6.65* 10^5 m`

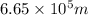
Step-by-step explanation:

We are given that

Magnetic field=B=
`4* 10^(-8) T`

`v=2.7* 10^7 m/s`

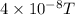
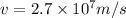
We have to find the height of proton from the surface of the Earth.

Mass of proton,
`m_p=1.67* 10^(-27) kg`

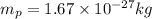
Charge on proton,
`q=1.6* 10^(-19) C`

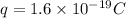
Radius of Earth, r=
`6.38* 10^6 m`

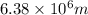
Centripetal force due to rotation of proton=
`(mv^2)/(r+h)`

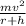
Magnetic force,F=
`qvB`

`(mv^2)/(r+h)=qvB`

`(mv)/(r+h)=qB`

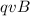
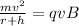
Substitute the values

`(1.67* 10^(-27)* (2.7* 10^7))/(6.38* 10^6+h)=1.6* 10^(-19)* 4* 10^(-8)`

`6.38*10^6+h=(1.67* 10^(-27)* 2.7* 10^7)/(1.6* 10^(-19)* 4* 10^(-8))`

`6.38*10^6+h=7.045* 10^6`

`h=7.045* 10^6-6.38* 10^6`

`h=0.665* 10^6=6.65* 10^5 m`