Question

The probability that a person with certain symptoms has hepatitis is 0.70.7. The blood test used to confirm this diagnosis gives positive results for 9292​% of people with the disease and 55​% of those without the disease. What is the probability that an individual who has the symptoms and who reacts positively to the test actually has​ hepatitis?

Answer 1

Therefore the probability that an individual who has the symptoms and reacts positively to test actually positively is 0.98.

Explanation:

Bayes' Theorem:

`P(A|B)=(P(B|A).P(A))/(P(B))`

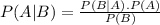
A,B = events

P(A|B)= probability of A given B is true

P(A),P(B)= the independent probabilities of A and B.

In this case we use Bayes' Theorem (spacial case)

`P(F|E)=(P(F).P(E|F))/(P(F).P(E|F)+P(F').P(E|F'))`

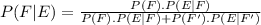
F= a person with symptoms has hepatitis

F'= a person with symptoms does have not hepatitis

E= Blood test positive.

P(F)= 0.7

P(F') = 1- 0.7 = 0.3

P(E|F)= 92% = 0.92

P(E|F')= 5%=0.05

`P(F|E)= (0.7 * 0.92)/((0.7 * 0.92)+(0.3 * 0.05))`

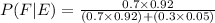
≈0.98

Therefore the probability that an individual who has the symptoms and reacts positively to test actually positively is 0.98.