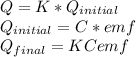Answer:
a) Q = C*emf
b) Reduction in electric field strength and electric potential
c) Initial current through the resistor = emf/R
d) The final charge = K*C*emf
Step-by-step explanation:
a) The resistors and capacitors are connected in series with the battery
Using Kirchoff's voltage law, sum of all voltages in the circuit is zero
Let
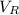 = Voltage dropped across the Resistor
= Voltage dropped across the Resistor
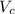 = Voltage dropped across the capacitor
= Voltage dropped across the capacitor
Applying KVL;
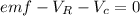 .........................(1)
.........................(1)
Since the connection is in series, the same current flow through the circuit

Putting
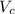 and
and
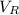 into equation (1)
into equation (1)
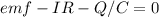
At the final charge, the capacitor in fully charged, and current drops to zero due to equilibrium
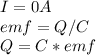
b) Current starts running through the plate because as the sheet of plastic is inserted between the plates both the electric field intensity and the electric potential reduces. The charge also reduces, then current flows
c) The current through the resistor is the current through the entire circuit ( series connection)

Putting the values of t and I₀ into the formula for I written above
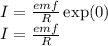
d) NB: The initial charge on the capacitor = C * emf
The final charge will be: