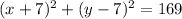Equation of a Circle
Circular equations are often organized in the following form:
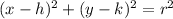
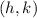 is where the circle is centered
is where the circle is centered
 is the radius
is the radius
To find the equation of a circle given its center and a point:
- Plug the center into the general equation as (h,k)
- Plug the given point into the general equation as (x,y)
- Solve for r²
- Plug (h,k) and r back into the original equation
Solving the Question
We're given:
- Center: (-7,7)
- Point: (-2,-5)
Plug the center into the general equation:
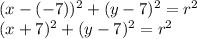
Plug in the given point (-2,-5) and find r²:
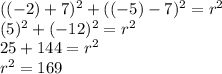
Plug the center and radius back into the original equation:
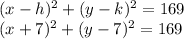
Answer