Answer:
The scores that are less than or equal to 10.8 are considered significantly low.
The scores that are greater than or equal to 32.4 are considered significantly high.
Explanation:
We are given the following information in the question:
Mean, μ = 21.6
Standard Deviation, σ = 5.4
We are given that the distribution of score is a bell shaped distribution that is a normal distribution.
Formula:

Significantly low score:
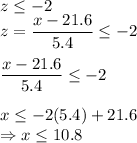
Thus, scores that are less than or equal to 10.8 are considered significantly low.
Significantly high score:
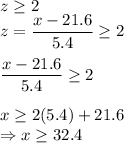
Thus, scores that are greater than or equal to 32.4 are considered significantly high.