Question

To anticipate the dip and hump in the road, the driver of a car applies her brakes to produce a uniform deceleration. Her speed is 100 km/h at the bottom A of the dip and 50 km/h at the top C of the hump, which is 120 m along the road from A. If the passengers experience a total acceleration of 3 m/s2 at A and if the radius of curvature of the hump at C is 150 m, calculate the radius of curvature rho at A.

Answer 1

Therefore the radius of curvature at A is 432.03 m.

Explanation:

Radius of curvature : If an object moves in curvilinear motion, then any point of the motion, the radius of circular arc path which best approximates the curve at that point is called radius of curvature.

Radius of curvature =
`\rho = (V^2_p)/(a)`

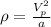
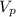`V_p`= velocity

a = acceleration perpendicular to velocity.

Velocity at the point A =
`V_A= 100 \ km/h`
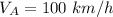
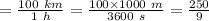`=(100 \ km)/(1 \ h)= (100* 1000 \ m)/(3600 \ s)=(250)/(9)` m/s

Velocity at the point C
`=V_C=50 \ km/ h=(125)/(9) \ m/s`

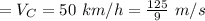
The distance between A and B is 120 m.

To find the declaration between the point A and C we use the following formula

`V^2_C=V^2_A+2a_ts`

`\Rightarrow( (125)/(9))^2=(\frac{250}9})^2+2a_t.120`

⇒
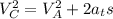
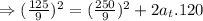
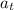`a_t` = -2.41 m/s²

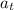`a_t`= tangential acceleration

Given the passengers experience a total acceleration of 3 m/s².

Total acceleration= 3 m/s².

`a = \sqrt{a^2_t+a^2_n`

`\Rightarrow a^2_n= a^2- a^2_t`

`\Rightarrow a_n=√(3^2-(-2.41)^2)`

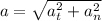
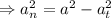
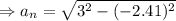
= 1.786 m/s²

Radius of curvature
`\rho_A=(V^2_A)/(a_n)`

`=(((250)/(9))^2)/(1.786)`

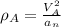
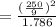
= 432.03 m

Therefore the radius of curvature at A is 432.03 m.