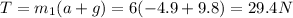Answer:
Acceleration=
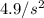
Tension=29.4 N
Step-by-step explanation:
We are given that
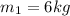
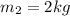
We have to find the magnitude of the acceleration of the two objects and the tension in the cord.
Tension,
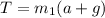
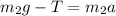
Substitute the values
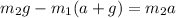
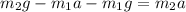
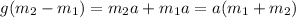
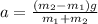
Substitute the values
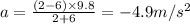
Where

Hence, the magnitude of the acceleration of the two objects =
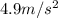
Substitute the values of a