Answer: Wavelength associated with the fifth line is 397 nm
Step-by-step explanation:

 = Wavelength of radiation
= Wavelength of radiation
E= energy
For fifth line in the H atom spectrum in the balmer series will be from n= 2 to n=7.
Using Rydberg's Equation:
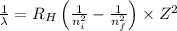
Where,
 = Wavelength of radiation
= Wavelength of radiation
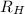 = Rydberg's Constant =
= Rydberg's Constant =

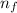 = Higher energy level = 7
= Higher energy level = 7
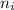 = Lower energy level = 2 (Balmer series)
= Lower energy level = 2 (Balmer series)
Putting the values, in above equation, we get
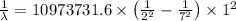
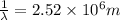

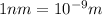
Thus wavelength λ associated with the fifth line is 397 nm