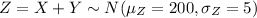Question

Dr. Sabbaghi is taking two flights today. The flight time for the first flight is Normally distributed with a mean of 90 minutes and a standard deviation of 3 minutes. The flight time for the second flight is Normally distributed with a mean of 110 minutes and a standard deviation of 4 minutes. His total flight time today has what type of distribution with what mean and standard deviation?

Answer 1

`E(Z) = E(X+Y) = E(X) +E(Y) = \mu_X +\mu_Y = 90+110=200`

`Var(Z) = Var(X+Y) = Var(X) +Var(Y) +2 Cov(X,Y)`

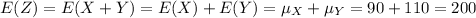
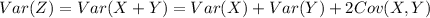
Since X and Y are independent then
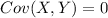`Cov(X,Y) =0` and we have this:

`Var(Z)= \sigma^2_X +\sigma^2_Y = 3^2 +4^2 = 9+16 =25`

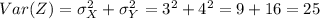
And the deviation would be given by:

`Sd(Z) = √(25)= 5`

And then the distribution for the total time would be given by:

`Z= X+Y \sim N( \mu_Z= 200, \sigma_Z= 5)`

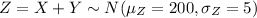
Explanation:

For this case we can assume that X represent the flight time for the first filght and we know that:

`X \sim N (\mu_X= 90. \sigma_x =3)`

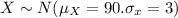
And let Y the random variable that represent the time for the second filght and we know this:

`Y \sim N(\mu_Y = 110, \sigma_Y =4)`

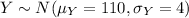
And we can define the random variable Z= X+Y as the total time for the two flights.

We can asume that X and Y are independent so then we have this:

`E(Z) = E(X+Y) = E(X) +E(Y) = \mu_X +\mu_Y = 90+110=200`

`Var(Z) = Var(X+Y) = Var(X) +Var(Y) +2 Cov(X,Y)`

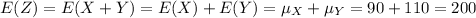
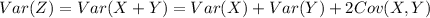
Since X and Y are independent then
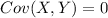`Cov(X,Y) =0` and we have this:

`Var(Z)= \sigma^2_X + \sigma^2_Y = 3^2 +4^2 = 9+16 =25`

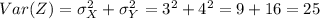
And the deviation would be given by:

`Sd(Z) = √(25)= 5`

And then the distribution for the total time would be given by:

`Z= X+Y \sim N( \mu_Z= 200, \sigma_Z= 5)`