Answer:
Probability that the weight will be less than 4293 grams is 0.8133.
Explanation:
We are given that weights of newborn baby boys born at a local hospital are believed to have a normal distribution with a mean weight of 4004 grams and a variance of 103,684.
Let X = weight of newborn baby boys
So, X ~ N(
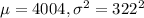 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean
= population mean
 = population standard deviation
= population standard deviation
(a) Probability that weight will be less than 4293 grams is given by = P(X < 4293 grams)
P(X < 4293) = P(
 <
<
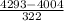 ) = P(Z < 0.89) = 0.8133
) = P(Z < 0.89) = 0.8133
Therefore, if a newborn baby boy born at the local hospital is randomly selected, probability that the weight will be less than 4293 grams is 0.8133.