Question

There is a 14 percent chance that a Noodles & Company customer will order bread with the meal. Use Excel to find the probability that in a sample of 10 customers (a) More than five will order bread. (Round your answer to 5 decimal places.) P(X > 5) (b) No more than two will. (Round your answer to 4 decimal places.) P(X ≤ 2) (c) None of the 10 will order bread. (Round your answer to 4 decimal places.) P(X = 0)

Answer 1

(a) P(X > 5) = 0.00095

(b) P(X
`\leq` 2) = 0.8455

(c) P(X = 0) = 0.2213

Explanation:

We are given that there is a 14 percent chance that a Noodles & Company customer will order bread with the meal.

The above situation can be represented through Binomial distribution;

`P(X=r) = \binom{n}{r}p^(r) (1-p)^(n-r) ; x = 0,1,2,3,.....`

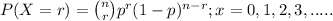
where, n = number of trials (samples) taken = 10 customers

r = number of success

p = probability of success which in our question is % that a Noodles

& Company customer will order bread with the meal, i.e., 14%

LET X = Number of customer that will order bread

Also, it is given that a sample of 26 customers is taken,

So, it means X ~
`Binom(n=10, p=0.14)`

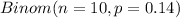
(a) Probability that more than five customer will order bread = P(X > 5)

P(X > 5) = P(X = 6) + P(X = 7) + P(X = 8) + P(X = 9) + P(X = 10)

=
`\binom{10}{6}0.14^(6) (1-0.14)^(10-6) + \binom{10}{7}0.14^(7) (1-0.14)^(10-7) +\binom{10}{8}0.14^(8) (1-0.14)^(10-8) +\binom{10}{9}0.14^(9) (1-0.14)^(10-9) +\binom{10}{10}0.14^(10) (1-0.14)^(10-10)`

=
`210 * 0.14^(6) * 0.86^(4) +120 * 0.14^(7) * 0.86^(3) +45 * 0.14^(8) * 0.86^(2) +10 * 0.14^(9) * 0.86^(1) +1 * 0.14^(10) * 0.86^(0)`

=
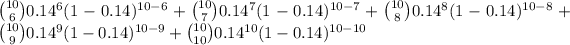
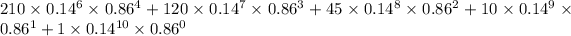
`9.505 * 10^(-4)` = 0.00095

(b) Probability that no more than two customer will order bread = P(X
`\leq` 2)

P(X
`\leq` 2) = P(X = 0) + P(X = 1) + P(X = 2)

=
`\binom{10}{0}0.14^(0) (1-0.14)^(10-0) + \binom{10}{1}0.14^(1) (1-0.14)^(10-1)+\binom{10}{2}0.14^(2) (1-0.14)^(10-2)`

=
`1 * 1 * 0.86^(10) +10 * 0.14 * 0.86^(9) +45 * 0.14^(2) * 0.86^(8)`

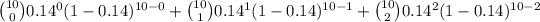
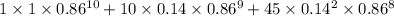
= 0.8455

(c) Probability that None of the 10 will order bread = P(X = 0)

P(X = 0) =
`\binom{10}{0}0.14^(0) (1-0.14)^(10-0)`

=
`1 * 1 * 0.86^(10)` = 0.2213

Answer 2

(a) More than five will order bread. P(X > 5)=0.0094

(b) No more than two will. P(X≤2)=0.8455

(c) None of the 10 will order bread. P(X=0)=0.2213

Explanation:

In this problem we should use a binomial distribution with p=0.14 and n=10.

a) P(X>5)

`P(X>5)=1-(P(0)+P(1)+P(2)+P(3)+P(4)+P(5))\\\\\\P(0)=\binom{10}{0}p^(0)(1-p)^(10)=1*1*0.2213=0.2213\\\\P(1)=\binom{10}{1}p^(1)(1-p)^(9)=10*0.14*0.25733=0.36026\\\\P(2)=\binom{10}{2}p^(2)(1-p)^(8)=45*0.0196*0.29922=0.26391\\\\P(3)=\binom{10}{3}p^(3)(1-p)^(7)=120*0.00274*0.34793=0.11457\\\\P(4)=\binom{10}{4}p^(4)(1-p)^(6)=210*0.00038*0.40457=0.03264\\\\P(5)=\binom{10}{5}p^(5)(1-p)^(5)=252*0.00005*0.47043=0.00638\\\\\\P(X>5)=1-(0.2213+0.36026+0.26391+0.11457+0.03264+0.00638)\\\\P(X>5)=1-0.99906=0.00094`

b) P(X≤2)

`P(X\leq2)=P(0)+P(1)+P(2)\\\\P(X\leq2)=0.22130+0.36026+0.26391=0.84547`

c) P(X=0)

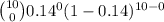
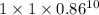`P(X=0)=P(0)=0.2213`