Answer:
(a) P(X > 262) = 0.30854
(b) P(227 < X < 257) = 0.49306
(c) P(X
 237) = 0.22663
237) = 0.22663
(d) Yes, a very preterm babies are unusual.
Explanation:
We are given that the lengths of a particular animal's pregnancies are approximately normally distributed, with mean = 252 days and standard deviation = 20 days.
Let X = lengths of a particular animal's pregnancies
So, X ~ N(
 )
)
The z score probability distribution is given by;
Z =
 ~ N(0,1)
~ N(0,1)
where,
 = population mean
= population mean
 = population standard deviation
= population standard deviation
(a) Probability that pregnancies lasts more than 262 days is given by = P(X > 262)
P(X > 262) = P(
 >
>
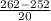 ) = P(Z > 0.5) = 1 - P(Z
) = P(Z > 0.5) = 1 - P(Z
 0.5)
0.5)
= 1 - 0.69146 = 0.30854
(b) Probability that pregnancies lasts between 227 and 257 days is given by = P(227 < X < 257) = P(X < 257) - P(X
 227)
227)
P(X < 257) = P(
 <
<
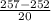 ) = P(Z < 0.25) = 0.59871
) = P(Z < 0.25) = 0.59871
P(X
 227) = P(
227) = P(


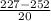 ) = P(Z
) = P(Z
 -1.25) = 1 - P(Z < 1.25)
-1.25) = 1 - P(Z < 1.25)
= 1 - 0.89435 = 0.10565
Therefore, P(227 < X < 257) = 0.59871 - 0.10565 = 0.49306
(c) Probability that a randomly selected pregnancy lasts no more than 237 days = P(X
 237)
237)
P(X
 237) = P(
237) = P(


 ) = P(Z
) = P(Z
 -0.75) = 1 - P(Z < 0.75)
-0.75) = 1 - P(Z < 0.75)
= 1 - 0.77337 = 0.22663
(d) Firstly, we will find the probability that gestation period is less than 202 days = P(X < 202)
P(X < 202) = P(
 <
<
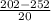 ) = P(Z
) = P(Z
 -2.5) = 1 - P(Z < 2.5)
-2.5) = 1 - P(Z < 2.5)
= 1 - 0.99379 = 0.00621
Since, we got a P(X < 202) of 0.00621 which is very small or nearly close to 0, so it means that Yes, a very preterm babies are unusual.