Question

In a survey of 450 adults 18 to 29 years of age, 419 said they use the Internet. In a survey of 400 adults 30 to 49 years of age, 324 said they use the internet. At a=0.01, can you reject the claim that the proportion of internet users is the same for two age groups?

Answer 1

Yes, we reject the claim that the proportion of internet users is the same for two age groups.

Explanation:

We are given that in a survey of 450 adults 18 to 29 years of age, 419 said they use the Internet. In a survey of 400 adults 30 to 49 years of age, 324 said they use the internet.

Let Null Hypothesis,
`H_0` :
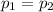`p_1 = p_2` or
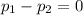`p_1 -p_2=0` {means that the proportion of internet users is the same for two age groups}

Alternate Hypothesis,
`H_1` :
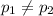`p_1 \\eq p_2` or
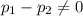`p_1 - p_2 \\eq 0` {means that the proportion of internet users is different for two age groups}

The test statistics that will be used here is Two sample proportion test;

T.S. =
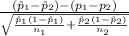`\frac{(\hat p_1 - \hat p_2) - (p_1 - p_2)}{\sqrt{(\hat p_1(1- \hat p_1))/(n_1) + (\hat p_2(1- \hat p_2))/(n_2) } }` ~ N(0,1)

where,
`p_1` = population proportion of internet users of first age group

`p_2` = population proportion of internet users of second age group

`\hat p_1` = proportion of internet users in a survey of 450 adults 18 to 29

years of age =
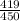`(419)/(450)` = 0.93

`\hat p_2` = proportion of internet users in a survey of 400 adults 30 to 49

years of age =
`(324)/(400)` = 0.81

`n_1` = sample of adults of age 18 to 29 years = 450

`n_2` = sample of adults of age 30 to 49 years = 400

So, test statistics =
`\frac{(0.93 - 0.81) - 0}{\sqrt{(0.93(1-0.93))/(450) + (0.81(1- 0.81))/(400) } }`

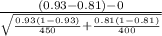
= 5.215

Now, at 0.01 significance level, the z table gives critical value of 2.5758. Since our test statistics is more than the critical value of z which means our test statistics will fall in the rejection region and we have sufficient evidence to reject our null hypothesis.

Therefore, we reject the claim that the proportion of internet users is the same for two age groups.

Answer 2

`z=\frac{0.931-0.81}{\sqrt{0.874(1-0.874)((1)/(450)+(1)/(400))}}=5.306`

`p_v =2*P(Z>5.306) =1.12x10^(-7)`

Comparing the p value with the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can conclude that the two proportions are different at 1% of significance

Explanation:

Data given and notation

`X_(1)=419` represent the number of adults that use internet between 18-29 years

`X_(2)=324` represent the number of adults that use internet between 30-49 years

`n_(1)=450` sample selected

`n_(2)=400` sample selected

`\hat p_(1)=(419)/(450)=0.931` represent the proportion of adults that use internet between 18-29 years

`p_(2)=(324)/(400)=0.81` represent the proportion of adults that use internet between 30-49 years

z would represent the statistic (variable of interest)

`p_v` represent the value for the test (variable of interest)

`\alpha=0.05` significance level given

Concepts and formulas to use

We need to conduct a hypothesis in order to check if is there is a difference between the two proportions, the system of hypothesis would be:

Null hypothesis:
`p_(1) - p_(2)=0`

Alternative hypothesis:
`p_(1)- p_(2) \\eq 0`

We need to apply a z test to compare proportions, and the statistic is given by:

`z=\frac{p_(1)-p_(2)}{\sqrt{\hat p (1-\hat p)((1)/(n_(1))+(1)/(n_(2)))}}` (1)

Where
`\hat p=(X_(1)+X_(2))/(n_(1)+n_(2))=(419+324)/(450+400)=0.874`

z-test: Is used to compare group means. Is one of the most common tests and is used to determine whether the means of two groups are equal to each other.

Calculate the statistic

Replacing in formula (1) the values obtained we got this:

`z=\frac{0.931-0.81}{\sqrt{0.874(1-0.874)((1)/(450)+(1)/(400))}}=5.306`

Statistical decision

Since is a two sided test the p value would be:

`p_v =2*P(Z>5.306) =1.12x10^(-7)`

Comparing the p value with the significance level given
`\alpha=0.05` we see that
`p_v<\alpha` so we can conclude that we have enough evidence to reject the null hypothesis, and we can conclude that the two proportions are different at 1% of significance