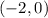The solutions of the system of equations are
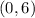 and
and
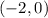
Step-by-step explanation:
Given that the system of equations are
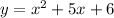 and
and
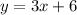
We need to determine the solution to the system of equations.
Let us determine the solution to the system of equations using substitution method.
Thus, we have,

Subtracting both sides of the equation by 6, we get,
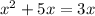
Subtracting both sides of the equation by 3x, we have,
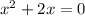
Simplifying, we get,
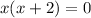
Thus, the values of x are
 and
and

Now, we shall determine the corresponding y - values.
Substituting
 in the equation
in the equation
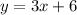 , we get,
, we get,
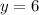
Similarly, substituting
 in the equation
in the equation
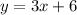 , we get,
, we get,

Therefore, the solution to the system of equations are
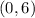 and
and