Question

The length of a bicycle pedal arm is 0.177 m, and a downward force of 145 N is applied to the pedal by the rider. What is the magnitude of the torque about the pedal arm's pivot when the arm is at an angle of (a)48.6°, (b) 90°, and (c) 180° with the vertical?

Answer 1

(a) 19.25 N-m

(b) 25.67 N-m

(c) 0 N-m

Step-by-step explanation:

Given:

Length of the pedal arm (L) = 0.177 m

Downward force
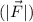`(|\vec{F}|)` = 145 N

Magnitude of torque is given by the formula:

`T=FL\sin\theta`

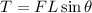
Where,
`\theta\to angle\ between\ F\ and\ L`

(a)

Given:

`\theta=48.6`°

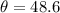Therefore, torque is given as:

`T=FL\sin\theta\\\\T=(145\ N)(0.177\ m)(\sin(48.6))\\\\T=19.25\ Nm`

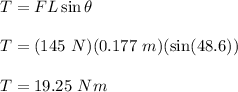
Therefore, the torque is 19.25 N-m.

(b)

Given:

`\theta=90`°

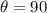Therefore, torque is given as:

`T=FL\sin\theta\\\\T=(145\ N)(0.177\ m)(\sin(90))\\\\T=25.67\ Nm`

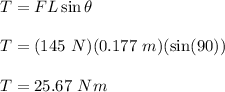
Therefore, the torque is 25.67 N-m.

(c)

Given:

`\theta=180`°

Therefore, torque is given as:

`T=FL\sin\theta\\\\T=(145\ N)(0.177\ m)(\sin(180))\\\\T=0\ Nm`

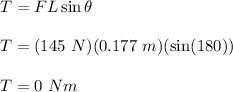
Therefore, the torque is 0 N-m.