Answer:
10044 N
Step-by-step explanation:
The acceleration of the cab is calculated using the equation of motion:
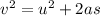
v is the final velocity = 0 m/s in this question, since it is brought to rest
u is the initial velocity = 10 m/s
a is the acceleration
s is the distance = 35 m
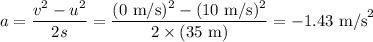
Since it accelerates downwards, its resultant acceleration is
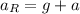
g is the acceleration of gravity.
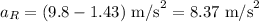
The tension in the cable is
