Question

A block of mass m begins at rest at the top of a ramp at elevation h with whatever PE is associated with that height. The block slides down the ramp over a distance d until it reaches the bottom of the ramp. How much of its original total energy (in J) survives as KE when it reaches the ground? (In other words, the acceleration is not zero like it was in lab and friction does not remove 100% of the original PE. How much of that original energy is left over after the friction does work to remove some?) m = 2.9 kg h = 2.2 m d = 5 m μ = 0.3 θ = 36.87°

Answer 1

The original energy that is left over after the friction does work to remove some is 33.724 J

Step-by-step explanation:

The original energy that is left in the system can be obtained by removing the energy loss in the system.

Given the mass m = 2.9 kg

the height h = 2.2 m

the distance d = 5 m

coefficient of friction μ = 0.3

θ = 36.87°

g = 9.8 m/
`s^(2)`

Since the block is at rest the initial energy can be expressed as;

`E_(i) = mgh`

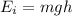
= 2.9 kg x 9.8 m/
`s^(2)` x 2.2 m

= 62.524 J

The energy loss in the system can be obtained with the expression below;

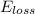`E_(loss)` = (μmgcosθ) x d

The parameters have listed above;

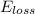`E_(loss)` = 0.3 x 2.9 kg x 9.8 m/
`s^(2)` x cos 36.87° x 5 m

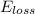`E_(loss)` = 28.8 J

The original energy that is left over after the friction does work to remove some can be express as;

`E = E_(i) -E_(loss)`

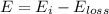
E = 62.524 J - 28.8 J

E = 33.724 J

Therefore the original energy that is left over after the friction does work to remove some is 33.724 J