Question

Neil is a drummer who purchases his drumsticks online. When practicing with the newest pair, he notices they feel heavier than usual. When he weighs one of the sticks, he finds that it is 2.33 oz. The manufacturer's website states that the average weight of each stick is 1.75 oz with a standard deviation of 0.22 oz. Assume that the weight of the drumsticks is normally distributed. What is the probability of the stick's weight being 2.33 oz or greater

Answer 1

The probability of the stick's weight being 2.33 oz or greater is 0.0041 or 0.41%.

Explanation:

Given:

Weight of a given sample (x) = 2.33 oz

Mean weight (μ) = 1.75 oz

Standard deviation (σ) = 0.22 oz

The distribution is normal distribution.

So, first, we will find the z-score of the distribution using the formula:

`z=(x-\mu)/(\sigma)`

Plug in the values and solve for 'z'. This gives,

`z=(2.33-1.75)/(0.22)=2.64`

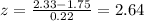
So, the z-score of the distribution is 2.64.

Now, we need the probability
`P(x\geq 2.33 )=P(z\geq 2.64)`.

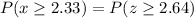From the normal distribution table for z-score equal to 2.64, the value of the probability is 0.9959. This is the area to the left of the curve or less than z-score value.

But, we need area more than the z-score value. So, the area is:

`P(z\geq 2.64)=1-0.9959=0.0041=0.41\%`

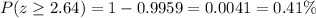
Therefore, the probability of the stick's weight being 2.33 oz or greater is 0.0041 or 0.41%.