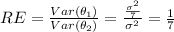Answer:
a) In order to check if an estimator is unbiased we need to check this condition:
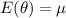
And we can find the expected value of each estimator like this:
![E(\theta_1 ) = (1)/(7) E(X_1 +X_2 +... +X_7) = (1)/(7) [E(X_1) +E(X_2) +....+E(X_7)]= (1)/(7) 7\mu= \mu](https://img.qammunity.org/2021/formulas/mathematics/college/xjzettgtc3t75mh1fzw9banrr17c0euuhm.png)
So then we conclude that
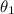 is unbiased.
is unbiased.
For the second estimator we have this:
![E(\theta_2) = (1)/(2) [2E(X_1) -E(X_3) +E(X_5)]=(1)/(2) [2\mu -\mu +\mu] = (1)/(2) [2\mu]= \mu](https://img.qammunity.org/2021/formulas/mathematics/college/k2x4wl2ray3dd2u7ws7zunsjgna86ue0ll.png)
And then we conclude that
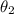 is unbiaed too.
is unbiaed too.
b) For this case first we need to find the variance of each estimator:
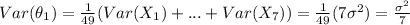
And for the second estimator we have this:
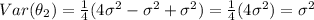
And the relative efficiency is given by:
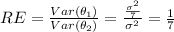
Explanation:
For this case we assume that we have a random sample given by:
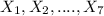 and each
and each
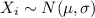
Part a
In order to check if an estimator is unbiased we need to check this condition:
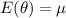
And we can find the expected value of each estimator like this:
![E(\theta_1 ) = (1)/(7) E(X_1 +X_2 +... +X_7) = (1)/(7) [E(X_1) +E(X_2) +....+E(X_7)]= (1)/(7) 7\mu= \mu](https://img.qammunity.org/2021/formulas/mathematics/college/xjzettgtc3t75mh1fzw9banrr17c0euuhm.png)
So then we conclude that
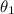 is unbiased.
is unbiased.
For the second estimator we have this:
![E(\theta_2) = (1)/(2) [2E(X_1) -E(X_3) +E(X_5)]=(1)/(2) [2\mu -\mu +\mu] = (1)/(2) [2\mu]= \mu](https://img.qammunity.org/2021/formulas/mathematics/college/k2x4wl2ray3dd2u7ws7zunsjgna86ue0ll.png)
And then we conclude that
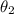 is unbiaed too.
is unbiaed too.
Part b
For this case first we need to find the variance of each estimator:
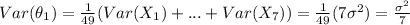
And for the second estimator we have this:
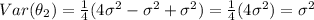
And the relative efficiency is given by: