Question

Find a real number c such that x^(2)+12x+c is a perfect square trinomial.

Answer 1

The value of c is 36

Explanation:

Now, we fine the perfect square polynomial, we need to have the expression of the form:

`a^2+b^2+2ab`

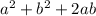
so this can be written as a perfect square as:
`a^2+b^2+2ab= (a+b)^2`

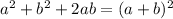
Now the expression given to us is:

`x^(2)+12x+c`

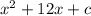
so when c is 36, we will get:

`x^(2)+12x+c= x^(2)+12x+36`

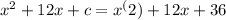
Now, this can be re-written as:

`x^(2)+2*6*x+6^2`

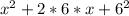
so here we can see that it is of the form:

`a^2+b^2+2ab`

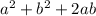
so the perfect square is:

`x^(2)+2*6*x+6^2= (x+6)^2`

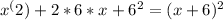
Hence, when c = 36 we get a perfect square.