Question

The length of a rectangle is increasing at a rate of 8 cm/s and its width is increasing at a rate of 5 cm/s. When the length is 13 cm and the width is 10 cm, how fast is the area of the rectangle increasing?

Answer 1

145 cm²/s

Step-by-step explanation:

Let the length be 'L', width be 'w' and area be 'A' at any time 't'.

Given:

Rate of increase of length is,
`(dL)/(dt)=8\ cm/s`

Rate of increase of width is,
`(dw)/(dt)=5\ cm/s`

Area of the rectangle is given as:

`A=Lw`

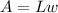
Differentiating both sides with respect to time 't', we get;

`(dA)/(dt)=(d)/(dt)(Lw)\\\\(dA)/(dt)=w(dL)/(dt)+L(dw)/(dt)`

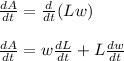
Now, we need to find the rate of area increase when L = 13 cm and w = 10 cm. So, plug in all the given values and solve for
`(dA)/(dt)`. This gives,

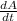`(dA)/(dt)=(10)(8)+(13)(5)\\\\(dA)/(dt)=80+65=145\ cm^2/s`

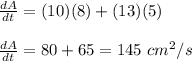
Therefore, the area is increasing a a rate of 145 cm²/s.